Jövőbe tekintő sorozat 9. rész: Az időutazás - 2. rész
- Írta: MikeReem
- 2006. augusztus 29.
Link másolása
A Jövőbe Tekintő előző részében kezdtünk foglalkozni az időutazás kérdésével, de csak az alapozásig jutottunk, ami persze nagyon fontos. Megtudhattuk, hogy a múltba való visszautazáskor komoly problémával találjuk magunkat szemben, mégpedig a nagypapa-paradoxonnal. Ugyanakkor néhány példán keresztül megértettük, hogy a világról alkotott szabályaink folytonos pontosításra szorulnak, így erre a paradoxonra is talán lesz megoldás. A lehetőségekről alant olvashattok.
Utazás a jövőbe
Mielőtt a múltba való utazással foglalkoznánk, tekintsünk egy kicsit a jövőbe utazás felé, hiszen erről még nem ejtettem szót. Nos ez az időutazás egyszerűbb fajtája. Hogy miért is? Azért mert az idő magától is előre halad, így ha úgy vesszük, mindnyájan időutazók vagyunk és a jövőbe utazunk állandóan. A valódi időutazástól csak annyi az eltérés, hogy a hétköznapokban az időutazó sajátideje együtt halad az abszolút idővel, míg sokkal érdekesebb lenne, ha a sajátidő jelentősen lassabban telne, mint az univerzális idő.
A jövő felé irányuló időutazás azért is tekinthető könnyebb feladatnak, mert jelentősen kevesebb probléma, paradoxon merül fel, ellentétben a fordított irányú utazással. Illetve ha csak a jövőbe való utazás létezne és múltba nem, akkor választ is kapnánk sok kérdésre, például, hogy miért nem jött már valaki a jövőből vissza, hogy elárulja az időutazás titkát, de erre még visszatérek.
Arra a kérdésre, hogy valóban eltérhet-e a sajátidő az abszolút időtől - mely nyilván az időutazás alapkelléke - maga Einstein adta meg a választ 1905-ben egy a speciális relativitás elméletet megalapozó cikkében. Felhívta a figyelmet egy különös következményre, mégpedig arra, hogy az igen nagy sebességgel mozgó test sajátideje lassabban telik, mint az egy helyben maradotté. Ez az idődilatációval magyarázható, matematikailag, fizikailag pedig teljesen korrekt a bizonyítása. Népszerű példa a jelenséggel kapcsolatban az utazó iker problémája: él két iker a Földön, közülük azonban az egyik elindul egy űrhajóval a világűr egy távoli pontja felé a fénysebességhez közeli sebességgel. Mikor visszatér jópár évnyi utazás után, meglepve tapasztalja, hogy ikertestvére sokkal öregebb nála.
A gyakorlatban persze igen nehezen következik be az ehhez szükséges sebességkülönbség, de matematikailag be lehet látni az elmélet helyességét. Tegyük fel, hogy az utazó testvér a fénysebesség 80%-ával utazik (persze jobb lenne fénysebességgel, vagy annál is gyorsabban, de mint tudjuk a fénysebességet lehetetlen elérni, azért is, mert ott végtelen lenne a tömegünk és zérus a térfogatunk, ami a legnagyobb jóindulattal sem nevezhető kényelmes állapotnak), a távolság pedig 10 fényév. Ekkor a Földről szemlélve az űrhajós 25 évig utazik (mert ugye oda-vissza tart az út). Az utazó sajátidejét a Lorentz-transzformációval számolhatjuk ki (aminek részletezését most mellőzök), az pedig mindössze 15 év. Vagyis ezekkel az értékekkel számolva 10 évet utazott előre az időben, ha a különbséget tekintjük.
Einstein elméletét jópáran megakarták cáfolni, mégpedig épp a relativitás elmélettel: e szerint a Földön maradt testvér idejéhez képest a gyors mozgást végző testvér ideje lassabban telik, ha viszont az űrhajón lévő testvér koordináta rendszeréhez viszonyítunk, akkor ő marad egyhelyben, míg a Föld távolodik, majd közeledik nagyon gyorsan. Tehát épp az ott maradottaknak kellene, hogy lassabban teljen az idő. Ez a feltételezés azonban hamis, ugyanis a speciális relativitás elméletben nem modellezhető a második eset, mert a hajóhoz rögzített koordinátarendszer nem inerciarendszer (először negatív és utána pozitív a gyorsulás). De az egyidejűséggel is magyarázható, hiszen az egyidejűség maga is relatív és a viszonyítási rendszertől függ, hogy a négydimenziós téridő melyik dimenziója felel meg a jelennek. Abban az esetben pedig, ha az űrhajót vesszük viszonyítási alapnak, akkor megfordulás után megváltozik a rajta lévő utas számára az egyidejűség fogalma, ebből pedig hibás levezetéshez jutunk.
Az elmélet gyakorlati helyességét egyébként 1939-ben elemi részecskéknél ki is mutatták, de a sokkal kézzelfoghatóbb kísérletre 1972-ben került sor. Ekkor J. C. Hafele és Richard E. Keating fizikusok nanoszekundum pontossággal járó atomórákat mozgattak. Az órák egymás mellett pontosan együtt jártak, de miután egyet egy nyugat felé, egy másikat pedig egy kelet felé haladó nagyon gyors repülőgépre helyeztek, landolás után megfigyelhető volt a Földön maradott órától való eltérés: a keletre mozgatott 59 nanoszekundumot késett, a nyugtra mozgatott pedig 273 nanoszekundumot sietett (ez ugye a Föld forgásának irányával megegyező, illetve ellentétes mozgásból adódott).
Ez az elmélet tehát nem csak elméletileg, hanem gyakorlatilag is lehetséges, csak a technikai tudásunk szab korlátot az időutazás mértékének. A lehetőségek viszont ettől eltekintve is korlátozottak lennének, hiszen egy igazán jó időutazást úgy képzelünk el, hogy néhány perc alatt akár évszázadokat is utazunk előre, ez viszont gyakorlatilag lehetetlennek tűnik ezzel a módszerrel. Ennek testvére lehetne a hibernálás, hiszen ugyanazt az eredményt érhetnénk el azzal is, csak úgy sokkal nagyobb időtávolságot utazhatnánk. Mégis valamiért a hibernálásra nem úgy gondol az ember, mint időutazásra és véleményem szerint az idődilatációs elmélettel is ez a helyzet. Ennek az lehet az oka, hogy az idő irányával megegyező a jövőbe való utazás iránya is és csak a múltba utazással együtt éreznénk hasznát. Hiszen akkor sokkal érdekesebb lenne, ha előre utaznánk néhány évet, majd vissza az eredeti időnkbe. Abban viszont nem kételkedem, hogy ha sikerül valamilyen elfogadható mértékben használni az idődilatációból adódó sajátidő eltérést, akkor az emberek azt is használni fogják. Elég csak arra gondolni, hogyha az utazó iker beteszi minden pénzét a bankba, akkor a számára 15 éves idő után a pénze 25 évnyit kamatozott.
Nyilván ez igen hasznos lehetőség lenne, ha igen nagy mértékben tudnánk előreugorni az időben. Ehhez nagy segítségünkre lenne, ha a fénynél is gyorsabban tudnánk mozogni. Érdemes megemlíteni azt a lehetőséget, hogy mi történik, ha egymással ellentétes irányú mozgásokat hasonlítunk össze. Vegyünk például két egymással szembe haladó autót az úton, amikor elhaladnak egymás mellett. Ha mindkettő 100 km/h-val halad, akkor akármelyikből is nézzük, a másik 200 km/h-val fog elsuhanni mellettünk. A fény sebessége, mint tudjuk 300 000 km/s. Mi történik, ha vele szembe haladunk egy 100 000 km/s-mal haladó űrhajóval? Akkor az űrhajóból nézve a fény 400 000 km/s-mal halad és ezek szerint meghaladja a meghaladhatatlannak vélt fénysebességet? Nem. Kísérletekkel bizonyították, hogy a fénnyel szembe, vagy vele azonos irányba mozogva is a fény sebességét mérve 300 000 km/s-mos értéket kapunk. Azaz 300 000 + 100 000 = 300 000 és 300 000 - 100 000 = 300 000. Ez matematikailag helytelennek tűnik, de mégis így van. Ezek szerint nem a világgal van a baj, hanem a matematikánkkal, így át is alakították kicsit azt. A relativitás elméletben szereplő idevonatkozó ügyes képlet szerint (melyet most szintén nem részletezek) ha például 270 000 km/s-mot adunk 270 000 km/s-hoz, akkor 298 350 km/s-ot kapunk, három fénysebességet összeadva is csak egy fénysebességet kapunk. Így már matematikailag is felülmúlhatatlan lett a fénysebesség.
Az idő dimenzióiról
Ha elszakadunk a megszokott tér és idő felfogástól, akkor azonban lehetőségünk nyílik egy valódi időutazásra, mely történhet múltba és jövőbe egyaránt. Mostani nézeteink szerint a tér három dimenziója és az idő egy dimenziója szoros kapcsolatban áll, elég ha felidézzük Lenin szavait: "Nincs semmi a világon, csak a mozgásban lévő anyag, a mozgásban lévő anyag pedig nem mozoghat másképp, mint térben és időben". Hogyan is utazhatnánk vissza az időben? Hisz akkor a térben minden testnek és folyamatnak is vissza kellene alakulnia, ami lehetetlen. Ez így is van, ha ragaszkodunk a jelenlegi téridő szemlélethez. Meg kell tehát próbálnunk kicsit másképpen gondolkodni. Ez kétség kívül nehéz, már a tér esetében is nehéz elképzelni a négy dimenziót, mert mi háromban élünk és ehhez vagyunk szokva. Vegyük azonban a következő példát, mely talán segít: egy 2 dimenziós világban egy szoba úgy néz ki, mint egy papírlapra rajzolt téglalap, melynek minden fala zárt. Ezen szobába zárt 2 dimenzióban élő ember vajon mekkora meglepetéssel fogadná, ha mi a papírra, a téglalapon belülre rajzolnánk egy asztalt. Mi egyszerűen átnyúlunk a 2 dimenziós fal felett, mert mi a harmadik dimenzióban is tudunk mozogni, de az ott élő 2 dimenziós ember azt tapasztalja mindebből, hogy a fal nem nyílt meg sehol, mégis a semmiből ott termett egy asztal. Képzeljük el ugyanezt a mi esetünkben. Egy zárt szobában vagyunk és ott terem egy asztal a szoba közepén, anélkül, hogy bárki bejött volna az ajtón, vagy akárhol. Bizony elég meglepő, de a negyedik dimenzióban mozogva épp így kerülhetnénk váratlan helyekre. Egyesek szerint a negyedik dimenzió létezése igenis valóság, melyre bizonyítékul szolgálnak a gömbvillámok, amik a negyedik dimenzió betüremkedései a mi dimenziónkba.
Az időt egy dimenziósnak ismerjük, melynek ráadásul iránya is van, így a térnél is nehezebb elképzelni több dimenziósnak, pedig az időutazáshoz szükségünk lesz rá. Ösztönösen megpróbálja az emberi agy a több dimenziós időt a tér több dimenziójához hasonlítani, ez azonban nem biztos, hogy helyes. Jó megközelítés lehet az, melyet a következő példával könnyebben meg lehet érteni: Képzeljünk el egy olyan ikerpárt, akiknek személyes időszerkezetük teljesen megegyezik, vagyis ugyanolyan korúak, mikor óvodába járnak, mikor elvégzik az iskolákat, mikor megkapják a diplomájukat, mikor összeházasodnak és épp ugyanannyi idősek mikor megszületik az első gyermekük, valamint ugyanannyi naposak, mikor meghalnak. Legyen ez a két testvér István és Béla. Az a furcsaság van kettejük kapcsolatában, hogy István úgy látja, hogy Bélával minden dupla olyan gyorsan történik. Ő még csak óvodás, mikor Béla iskolába jár, ő épphogy megkapja a diplomáját, de Bélának már gyerekei vannak és mire ő megházasodik, Béla jobb létre szenderült. Mintha Bélának fele annyi ideje lett volna élni, de István látta, hogy Bélával nemcsak gyorsabban történtek az események, hanem valóban gyorsabban is öregedett. Ez azonban nem elég: Béla mindezt pont fordítva látja. Úgy látja, hogy ő jár még épp iskolába, mikor István már a diplomáját veheti át, ő épp, hogy megházasodik, de István körül már az unokái futkosnak és míg ő csak az élete felén jár, ikertestvére már halott. Mindez úgy lehetséges, hogy a két ikertestvér különböző idődimenzióban él.
Mindkét testvér úgy látja, mintha a testvére csinálna mindent sokkal gyorsabban. Olyan, mintha egy mezőn két egymástól távol álló juhász nézne egymásra és mindkettő azt mondhatná a másikról, hogy milyen kicsi. Mindkettejüknek igaza van, hiszen a saját szemszögéből kicsinek látszik a másik, holott a valóságban aligha van köztük lényeges különbség. Ezen ikertestvéres példához készítettem egy ábrát, mely jól szemlélteti, hogy hogyan kell elképzelni a kétdimenziós időt, melyen ebben az esetben csak két külön idősíkot ábrázoltam, de végtelen lehetséges. Minél nagyobb az általuk bezárt szög, annál nagyobb az eltérés mértéke.
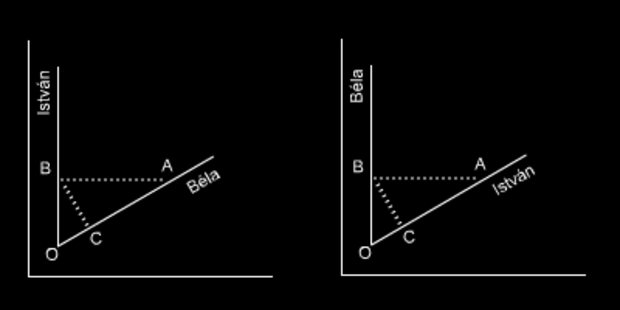
A képen látható mindkét testvér szemszögéből a másik eltérése, melynek mértéke épp akkora, hogy egymást dupla sebességgel lássák öregedni. A baloldali esetben például Béla C éves korában úgy látja, hogy István már B éves, ahol B=2C. Ugyanakkor István B éves korában Bélát A évesnek látja, ahol A=2B.
Az idő ilyen dimenzionálásával viszonylag egyszerűen lehetséges az időutazás: pusztán dimenziót kell váltani. A bal oldali szemszög szerint Béla úgy tud visszautazni a múltba, hogy A (legyen ez 32) éves korában indul István dimenziójába. Ekkor Bélának úgy tűnik, hogy István 2A (64) éves. Mikor odaér, akkor azonban nem a 64 éves Istvánnal találkozik, hanem a B (16) évessel. Ennek az az oka, hogy Istvánhoz a 32 éves Béla csak 16 éves korában érkezhet meg, hiszen István szemszögéből Béla öregszik dupla olyan gyorsan. Ugyanez történik, mikor Béla visszatér a saját dimenziójába: Csak akkor hagyhatta ott a 16 éves Istvánt, mikor Béla saját idődimenziójában 8 év telt el születése óta. Vagyis Béla visszajut a saját dimenziójába, indulásához képest 24 évvel korábbra (ekkor volt ő eredetileg 8 éves). Béla így az A-B-C utat teszi meg, ha a bal oldali ábrát tekintjük.
Persze ha végtelen idősík létezik, akkor tetszőleges lehet az időutazás távolsága, pusztán az idősíkok által bezárt szöget kell variálni.
Most már úgy is vehetjük, hogy megtaláltuk a múltba való időutazás egy lehetséges változatát, paradoxonok viszont továbbra is fennállnak. Azok kizárásához még tovább kell lépnünk a kétdimenziós idő szemléletünkről és a lehetséges időtopológiákkal kell foglalkoznunk. Mielőtt azonban ebbe belebonyolódnánk, tisztázzuk, hogy milyen problémák merülnek fel pontosan a múltba történő utazáskor. Először is tisztázni kell, hogy közvetlen kapcsolat nem lehet a külön idődimenziók között. Tehát a példában szereplő ikertestvérek nem léphetnének kapcsolatba egymással, csak időutazás révén. Elég arra gondolnunk, hogy ha a 32 éves Béla akar kérdezni valamit a 64 éves Istvántól, akkor a kérdést a 16 éves István kapja meg és válasza a 8 éves Bélához jut el. Itt pedig eljutunk a fő problémához, az ok okozati kapcsolat felborulásához. Vagyis Béla előbb kap választ, minthogy feltenné a kérdést: előbb következik be az okozat, mint az ok. A kétdimenziós idő feltétele tehát a visszafelé ható okság, legalábbis ha teljesen szabad időutazási lehetőségeket akarunk.
A filozófusok, amikor az időutazás és így a múltba történő utazás kapcsán felmerülő ellentmondásokról vitatkoztak, egy fontos megállapításra jutottak, mellyel kizárhatóvá tették a paradoxonok bekövetkeztét. Ez pedig az, hogyha az időt még nem is sikerült megismernünk teljesen és az többdimenziós, lehetővé téve az időutazást, akkor sem szeghetjük meg a világunk alapvető szabályait: nem tehetünk olyat, ami nem logikus (persze ezen lehetne vitatkozni, hogy az időutazás logikus-e, de több idődimenzió esetén igen). A térre egyszerű megérteni, hogy mi nem logikus: nem állhatok saját magam jobb oldalán, vagy nem lehetek saját magam szülője sem. Ha az időre is elfogadjuk ezeket a szabályokat, akkor nem következik be semmilyen ellentmondás. A nagypapa paradoxon esetén így ha visszautazik emberünk a múltba, hogy végezzen saját nagyapjával, akkor megpróbálhatja ugyan, de sikerülni semmiképpen sem fog neki (és másnak sem, egészen addig, amíg meg nem fogan hősünk szülője, aki majdan életet fog adni neki). Ezt azért köthetjük ki, mert eme tett legalább annyira nem felelne meg a logikának, mint a tér esetén említett példák.
A magyarázat elfogadhatónak tűnik, azt azonban észre kell vegyük, hogy ezzel jelentősen korlátozzuk a lehetőségeket. Ismét csak filozófiai kérdés, hogy ha vissza is tudunk utazni az időben, akkor ott mit tehetünk így? Ha ugyanis megpróbálunk csak szemlélőként ott járkálni, akkor is tudtunkon kívül befolyásolhatnánk dolgokat, amik eredetileg nem is történtek meg, vagyis szabályunk szerint nem változtathatjuk azt meg. Kérdés tehát, hogy mi számít változtatásnak. Például visszautazva a középkori Itáliába, miközben csodáljuk az ottani építészetet, az utcán meglát minket egy neves festő, aki aztán hazatérve emlékezetből megfesti a portrénkat. Vita tárgya máig is, hogy ebben az esetben a festmény valóban létezett valaha, csak mondjuk egy tűz miatt elpusztult és semmilyen feljegyzés nem maradt a létezéséről, vagy ezzel a tettel megváltoztatnánk a jövőt. Az idővel foglalkozó filozófusok egy része például úgy tartja, hogy a múlt nem is létezik, csak az emlékek által alkotott világ.
Ha a létezését nem is tagadjuk, de ezen elméletnek fontos része lehet az, hogy ha a múltban olyan tetteket hajtunk végre, amiknek következményeiről nem is tudunk, akkor semmi akadálya, hogy megtegyük. Ez alatt azt értem, hogy például nyilván nem lehetne visszautazni a második világháború kitörése elé néhány nappal, hogy megöljük Hitlert, mert ezzel jelentős változás történne a történelemben. Azt, viszont, hogy visszautazunk a dinoszauruszok korába, már nehezebb kizárni. Elképzelhető ugyanis, hogy a jövőben megalkotja az emberiség az időgépet, melynek segítségével elkezdenek visszautazni a dinoszauruszok közé nézelődni, azok viszont felfalják az összes látogatót. Ezzel az állatok jóllaknak, de igazán nem változtat semmit a helyzeten az emberek látogatása, mert kipusztul az összes őshüllő, így jelenlegi világunkban semmit sem befolyásol az eset.
Vannak azonban, akik tiltakoznak az ilyesfajta engedmények ellen is és azt állítják, hogy ha a világban a legapróbb változás is történik, akkor már ha kicsit is, és látszólag lényegtelen mértékben is, de megváltoztatjuk az események eredeti alakulását. Képzeljük el, hogy visszautazunk az időben és semmi mást nem teszünk, mint egy helyben állunk néhány másodpercig, majd távozunk is. Amíg ott álltunk, letapostuk a lábunk alatt lévő füvet, melyet eredetileg senki sem taposott le, tehát változást indukáltunk a világban. Ez a nézet tehát teljesen kizárja az időutazás lehetőségét. Fogadjuk el azonban akármelyik lehetőséget - vannak engedmények, vagy nincsenek -, a teljesen szabad időutazáshoz nem elegendő a kétdimenziós idő, hiszen túl sok logikailag lehetetlen dologgal kerülünk szembe. Így jutunk el a három dimenziós időhöz.
Az idő topológiáiról
Ehhez meg kell ismerkednünk az idő topológiájával. Tisztázzuk először, hogy mi az a "topológia" (aki tanult diszkrét matematikát, attól elnézést kérek a múlt felhánytorgatása miatt). A definícióját inkább mellőzöm, mert annak megértése is igen sok matematikai fogalom ismeretét feltételezi. Egyszerűbb megérteni egy példán keresztül. A topológia egy olyan geometriai tulajdonság, ami az összes közül a legabsztraktabb, így a legnehezebb elképzelni. Amikor valaminek a topológiáját vizsgáljuk, akkor eltekintünk minden metrikus, vagyis mérhető tulajdonságától. Nem számít az alakja, a mérete az adott testnek. Gumigeometriának is hívják, ennek oka pedig egy gyakran felhozott példa. Képzeljünk el egy befőttes gumit, melyet különböző méretű üvegre húzhatunk, a guminak változni fog a mérete, de a topológiája változatlan marad. Az alakhoz sem köthetjük, hiszen ha a gumit egy szögletes tejes dobozra húzunk, akkor annak veszi fel az alakját, de a topologikus tulajdonsága ekkor sem változik. Ha azonban elszakad a befőttes gumi, akkor megváltozik a topológiája is. Ha a topologikus tulajdonsága szerint vizsgáljuk, akkor semmi különbség sincs egy gumicsirke és egy traktor között. Ezen elvont szemléletre lesz éppen szükségünk az idő vizsgálatakor, hiszen el kell tekinteni minden térhez köthető tulajdonságtól.
Az idő lehetséges topológiáit egy viszonylag egyszerű topologikus ábrázolási móddal szemléltetünk, mégpedig a gráfokkal. A gráfok pontokból állnak, melyeket vonalakkal köthetünk össze, ezen vonalakat nevezzük éleknek. Az éleket úgy adhatjuk meg, hogy mely két pontot köti össze. Létezik irányított és irányítatlan él, melyet nyíllal jelölünk. Az élek alakja lényegtelen. A modern kozmogónia elég sok különböző idő topológiával foglalkozik, de nekünk elegendő lesz a következő hárommal foglalkozni, ezeket láthatjátok a következő ábrán.

Balról jobbra haladva a következő elnevezéseket használjuk: nyíl, karika és fa topológia. Az élek hossza lényegtelen, legfeljebb az áttekinthetőséget segíti. Mint említettem az élek alakja is jelentéktelen, tehát a nyílnak nem kell, hogy egyenes legyen, a karikának nem kell, hogy szabályos kör legyen. A fának különleges tulajdonságai vannak. Éleit választhattam volna irányítottaknak is, jelölésben ekkor a nyilak mindig felfele mutattak volna, de hogy miért is irányítatlanok, azt majd később megtudjátok. Fontos, hogy a fát jelen esetben lentről felfele kell vizsgálnunk (igazából a gyökértől a levelek felé kell nézni). A fa gyökere nem lehet szerteágazó, tehát egy pontból ered, az elágazások végein elhelyezkedő pontokat pedig leveleknek nevezzük (ahonnan nincs további elágazás).
Megszereztük a szükséges elméleti hátteret, hogy végre elkezdhessünk az idő topológiájáról beszélni. A nyíl topológia az, ami a jelenleg elfogadott idő szemléletet tükrözi. Vagyis teljesen lineárisan haladunk előre az időben. Két elméletet különböztethetünk meg itt is: a statikus és a dinamikus időszemléletet. Az ábra segítségével jól érthető a kettő közötti különbség, ugyanis a statikus időszemlélet szerint, ahogy haladunk előre az időben, úgy haladunk a nyíl egy részén a vége felé. Tehát e szerint véges az idő: volt kezdete és a nyíl végét elérve meg fog szűnni. A dinamikus időszemlélet szerint folyamatosan a nyíl végén haladunk és ahogy telnek a percek, úgy hosszabbodik ez a képzeletbeli nyíl (ebben az esetben nem lehetséges a jövőbe való utazás).
A karika topológián, mint látszik a nyíl körkörösen mutat, tehát az idő szüntelenül ismétli önmagát. Ezen elméletet látszik igazolni a folyton táguló világegyetem, melyben egyesek szerint egy pont után bekövetkezik újra egy ősrobbanás és minden kezdődik elölről. Az időutazás problémája itt leegyszerűsödik (persze a paradoxonok okozta problémák maradnak): képzeljük csak el, hogy Budapestről Bécsbe nem csak nyugatra indulva juthatunk el, hanem keletre is, csak sokkal hosszabb utat kell megtennünk. Tehát a karika idő topológia esetében, ha képesek vagyunk utazni a jövőbe, akkor elég sokat utazva a múltba jutunk. Ez az eredmény viszont problémát is jelent, mert megszűnik a jövő és múlt közti különbség. Elég arra gondolni, hogyha a jövőről beszélünk, akkor az egyben a múltunk is, ugyanakkor a múltunk a jövőnk.
Másik nagy probléma a karika topológiával, hogy nem egyértelmű az idő iránya. Az ábrán ugyan bejelöltem egy irányt, de az akár fordított is lehetne. Meghatározni nehéz az idő irányát, ebben az esetben lehetetlen, legfeljebb kiköthetjük, hogy legyen óramutató járásával egyező, vagy ellentétes. Azért állítom, hogy lehetetlen ebben az esetben meghatározni az idő irányát, mert létezik erre egy általánosan elfogadott elv. Ez pedig a már egyszer említett ok-okozati rendszer. Elengedhetetlen, hogy valaminek az oka előbb történjék időben, mint az okozata. Az pedig kizárt, hogy két partikuláris esemény oka legyen egymásnak (a kauzális reláció aszimmetrikus). A karika topológia esélyei ezzel jelentősen lecsökkentek, hiszen nem határozható meg egyértelműen az ok-okozati rendszer.
Maradt még a fa topológia, melynél a nyílhoz hasonlóan nemhogy nem gond az idő irányának meghatározása, hanem egyedülállóan, jelölés nélkül is nagyon jól látszik (ezért nem szokás az éleket irányítottnak venni). Arra, hogy hol következik be elágazás, leginkább kétféle magyarázat van. Az egyik szerint a természet törvényei határozzák meg az elágazásokat. Ez végtelen sok elágazást tesz lehetővé, hisz akár ha egy atomot tekintünk egy időpillanatban, akkor az vagy osztódik, vagy nem. Rögtön egy elágazást találtunk.
A másik elmélet szerint pont fordítva van: az elágazások írják le a természet törvényeit. Ez rengeteg lehetőséget vet fel, többek között a bennünket érdeklő időutazást is. Mindez azonban csak akkor lehetséges, ha a dinamikus időszemléletet fogadjuk el. Képzeljük csak el, hogy a történelmünk sokáig egy vonalon halad. Aztán mikor megalkot az emberiség egy időgépet, akkor visszautaznak vele a múltba. Ott nyilván változást indukálnak ezzel, így egy külön ágat hoznak létre. A megváltoztatott történelem azon az ágon halad tovább, amiből elindultak, az pedig marad változatlan. Így már semmilyen paradoxon, vagy ellentmondás nem állja utunkat. Egyedüli gond, hogy mint említettem a dinamikus időfelfogás szerint folyamatosan alakítjuk a jövőt, így nem lehetséges a jövőbe történő időutazás. Statikus időfelfogásnál megengedett a jövőbe való utazás, de az idő nem lehet fa topológiájú.
Ha elegyítjük a kétdimenziós és a fa topológiájú idő elméletét, akkor juthatunk a három dimenziós időhöz. Képzeljük el, hogy István és Béla idősíkjai ugyanúgy helyezkednek el, csak éppen az egésznek van mélységi kiterjedése is, ahol a fa ágai terebélyesednek. Ezzel a szemlélettel már kedvünk szerint utazhatunk vissza a múltba, az általunk indukált változások hatására újabb, alternatív dimenziókat hozunk létre. Azzal viszont számolni kell, hogy a jövőbe nem tudunk visszautazni (hacsak nem hibernálással, vagy idődilatációval lepörgetjük a szükséges időt).
Epilógus
Összegezve az egész gondolatmenetet, valószínűleg kétféle szerkezete és felépítése lehet az időnek. Egyik felfogás szerint a ma is ismert tulajdonságai (statikus/dinamikus és nyíl topológiájú) már a valóságot mutatják és megváltoztathatatlanok. Másik felfogás szerint dinamikus és fa topológiájú, lehetővé téve a múltba való időutazást. Igazából egyikre sincs bizonyítékunk. Nyilván minden jel az első elmélet helyességét látszik igazolni, de amíg nincs bizonyíték a második ellen, addig nem vethetjük el azt sem. Márpedig bizonyíték nincs, mert a korábban említett "miért nem jöttek már vissza az időben, hogy elmondják az időgép titkát" kérdésekre egyszerű a válasz. Visszajöttek és az idő egy másik ágán már 2006-ban is használják az időgépet. Azt, hogy valójában melyik szemlélet a helyes, tudniillik létezik időutazás, vagy sem, a fizika és a tudomány fejlődése idővel nyilván eldönti. Addig viszont úgy gondolom, hogy elég nagy a világunk ahhoz, hogy találjon mindenki magának ismeretlent. Miért akarnánk addig más időbe utazni, amíg a sajátunk is elég rejtéllyel szolgál?
Felhasznált irodalom:
Lewis - The Paradoxes of Time Travel
Judith Jarvis Thomson - A kétdimenziós idő példája
Newton-Smith, Chin-Steenrod, McCall, Von Wright, Reichenbach, H. Mellor elméletei
Csaba György Gábor - Kalandozás az égbolton
Lenin összes művei
Űrhajózási Lexikon
Felix R. Paturi - A technika krónikája
A világ körülöttünk - Beszélgetések a világról és törvényeiről
Kulin György - Mit mondanak a csillagok
Egely György - A titokzatos gömbvillám
Albert Einstein - On the electrodynamics of moving bodies
Max von Laue - Das relativitätsprinzip
Peter Pesic - Einstein and the twin paradox
Kempelen Farkas Digitális Tankönyvtár
Ambrus Attila József - Itt és most (értekezés a térről és időről)
Mielőtt a múltba való utazással foglalkoznánk, tekintsünk egy kicsit a jövőbe utazás felé, hiszen erről még nem ejtettem szót. Nos ez az időutazás egyszerűbb fajtája. Hogy miért is? Azért mert az idő magától is előre halad, így ha úgy vesszük, mindnyájan időutazók vagyunk és a jövőbe utazunk állandóan. A valódi időutazástól csak annyi az eltérés, hogy a hétköznapokban az időutazó sajátideje együtt halad az abszolút idővel, míg sokkal érdekesebb lenne, ha a sajátidő jelentősen lassabban telne, mint az univerzális idő.
A jövő felé irányuló időutazás azért is tekinthető könnyebb feladatnak, mert jelentősen kevesebb probléma, paradoxon merül fel, ellentétben a fordított irányú utazással. Illetve ha csak a jövőbe való utazás létezne és múltba nem, akkor választ is kapnánk sok kérdésre, például, hogy miért nem jött már valaki a jövőből vissza, hogy elárulja az időutazás titkát, de erre még visszatérek.
Arra a kérdésre, hogy valóban eltérhet-e a sajátidő az abszolút időtől - mely nyilván az időutazás alapkelléke - maga Einstein adta meg a választ 1905-ben egy a speciális relativitás elméletet megalapozó cikkében. Felhívta a figyelmet egy különös következményre, mégpedig arra, hogy az igen nagy sebességgel mozgó test sajátideje lassabban telik, mint az egy helyben maradotté. Ez az idődilatációval magyarázható, matematikailag, fizikailag pedig teljesen korrekt a bizonyítása. Népszerű példa a jelenséggel kapcsolatban az utazó iker problémája: él két iker a Földön, közülük azonban az egyik elindul egy űrhajóval a világűr egy távoli pontja felé a fénysebességhez közeli sebességgel. Mikor visszatér jópár évnyi utazás után, meglepve tapasztalja, hogy ikertestvére sokkal öregebb nála.
A gyakorlatban persze igen nehezen következik be az ehhez szükséges sebességkülönbség, de matematikailag be lehet látni az elmélet helyességét. Tegyük fel, hogy az utazó testvér a fénysebesség 80%-ával utazik (persze jobb lenne fénysebességgel, vagy annál is gyorsabban, de mint tudjuk a fénysebességet lehetetlen elérni, azért is, mert ott végtelen lenne a tömegünk és zérus a térfogatunk, ami a legnagyobb jóindulattal sem nevezhető kényelmes állapotnak), a távolság pedig 10 fényév. Ekkor a Földről szemlélve az űrhajós 25 évig utazik (mert ugye oda-vissza tart az út). Az utazó sajátidejét a Lorentz-transzformációval számolhatjuk ki (aminek részletezését most mellőzök), az pedig mindössze 15 év. Vagyis ezekkel az értékekkel számolva 10 évet utazott előre az időben, ha a különbséget tekintjük.
Einstein elméletét jópáran megakarták cáfolni, mégpedig épp a relativitás elmélettel: e szerint a Földön maradt testvér idejéhez képest a gyors mozgást végző testvér ideje lassabban telik, ha viszont az űrhajón lévő testvér koordináta rendszeréhez viszonyítunk, akkor ő marad egyhelyben, míg a Föld távolodik, majd közeledik nagyon gyorsan. Tehát épp az ott maradottaknak kellene, hogy lassabban teljen az idő. Ez a feltételezés azonban hamis, ugyanis a speciális relativitás elméletben nem modellezhető a második eset, mert a hajóhoz rögzített koordinátarendszer nem inerciarendszer (először negatív és utána pozitív a gyorsulás). De az egyidejűséggel is magyarázható, hiszen az egyidejűség maga is relatív és a viszonyítási rendszertől függ, hogy a négydimenziós téridő melyik dimenziója felel meg a jelennek. Abban az esetben pedig, ha az űrhajót vesszük viszonyítási alapnak, akkor megfordulás után megváltozik a rajta lévő utas számára az egyidejűség fogalma, ebből pedig hibás levezetéshez jutunk.
Az elmélet gyakorlati helyességét egyébként 1939-ben elemi részecskéknél ki is mutatták, de a sokkal kézzelfoghatóbb kísérletre 1972-ben került sor. Ekkor J. C. Hafele és Richard E. Keating fizikusok nanoszekundum pontossággal járó atomórákat mozgattak. Az órák egymás mellett pontosan együtt jártak, de miután egyet egy nyugat felé, egy másikat pedig egy kelet felé haladó nagyon gyors repülőgépre helyeztek, landolás után megfigyelhető volt a Földön maradott órától való eltérés: a keletre mozgatott 59 nanoszekundumot késett, a nyugtra mozgatott pedig 273 nanoszekundumot sietett (ez ugye a Föld forgásának irányával megegyező, illetve ellentétes mozgásból adódott).
Ez az elmélet tehát nem csak elméletileg, hanem gyakorlatilag is lehetséges, csak a technikai tudásunk szab korlátot az időutazás mértékének. A lehetőségek viszont ettől eltekintve is korlátozottak lennének, hiszen egy igazán jó időutazást úgy képzelünk el, hogy néhány perc alatt akár évszázadokat is utazunk előre, ez viszont gyakorlatilag lehetetlennek tűnik ezzel a módszerrel. Ennek testvére lehetne a hibernálás, hiszen ugyanazt az eredményt érhetnénk el azzal is, csak úgy sokkal nagyobb időtávolságot utazhatnánk. Mégis valamiért a hibernálásra nem úgy gondol az ember, mint időutazásra és véleményem szerint az idődilatációs elmélettel is ez a helyzet. Ennek az lehet az oka, hogy az idő irányával megegyező a jövőbe való utazás iránya is és csak a múltba utazással együtt éreznénk hasznát. Hiszen akkor sokkal érdekesebb lenne, ha előre utaznánk néhány évet, majd vissza az eredeti időnkbe. Abban viszont nem kételkedem, hogy ha sikerül valamilyen elfogadható mértékben használni az idődilatációból adódó sajátidő eltérést, akkor az emberek azt is használni fogják. Elég csak arra gondolni, hogyha az utazó iker beteszi minden pénzét a bankba, akkor a számára 15 éves idő után a pénze 25 évnyit kamatozott.
Nyilván ez igen hasznos lehetőség lenne, ha igen nagy mértékben tudnánk előreugorni az időben. Ehhez nagy segítségünkre lenne, ha a fénynél is gyorsabban tudnánk mozogni. Érdemes megemlíteni azt a lehetőséget, hogy mi történik, ha egymással ellentétes irányú mozgásokat hasonlítunk össze. Vegyünk például két egymással szembe haladó autót az úton, amikor elhaladnak egymás mellett. Ha mindkettő 100 km/h-val halad, akkor akármelyikből is nézzük, a másik 200 km/h-val fog elsuhanni mellettünk. A fény sebessége, mint tudjuk 300 000 km/s. Mi történik, ha vele szembe haladunk egy 100 000 km/s-mal haladó űrhajóval? Akkor az űrhajóból nézve a fény 400 000 km/s-mal halad és ezek szerint meghaladja a meghaladhatatlannak vélt fénysebességet? Nem. Kísérletekkel bizonyították, hogy a fénnyel szembe, vagy vele azonos irányba mozogva is a fény sebességét mérve 300 000 km/s-mos értéket kapunk. Azaz 300 000 + 100 000 = 300 000 és 300 000 - 100 000 = 300 000. Ez matematikailag helytelennek tűnik, de mégis így van. Ezek szerint nem a világgal van a baj, hanem a matematikánkkal, így át is alakították kicsit azt. A relativitás elméletben szereplő idevonatkozó ügyes képlet szerint (melyet most szintén nem részletezek) ha például 270 000 km/s-mot adunk 270 000 km/s-hoz, akkor 298 350 km/s-ot kapunk, három fénysebességet összeadva is csak egy fénysebességet kapunk. Így már matematikailag is felülmúlhatatlan lett a fénysebesség.
Az idő dimenzióiról
Ha elszakadunk a megszokott tér és idő felfogástól, akkor azonban lehetőségünk nyílik egy valódi időutazásra, mely történhet múltba és jövőbe egyaránt. Mostani nézeteink szerint a tér három dimenziója és az idő egy dimenziója szoros kapcsolatban áll, elég ha felidézzük Lenin szavait: "Nincs semmi a világon, csak a mozgásban lévő anyag, a mozgásban lévő anyag pedig nem mozoghat másképp, mint térben és időben". Hogyan is utazhatnánk vissza az időben? Hisz akkor a térben minden testnek és folyamatnak is vissza kellene alakulnia, ami lehetetlen. Ez így is van, ha ragaszkodunk a jelenlegi téridő szemlélethez. Meg kell tehát próbálnunk kicsit másképpen gondolkodni. Ez kétség kívül nehéz, már a tér esetében is nehéz elképzelni a négy dimenziót, mert mi háromban élünk és ehhez vagyunk szokva. Vegyük azonban a következő példát, mely talán segít: egy 2 dimenziós világban egy szoba úgy néz ki, mint egy papírlapra rajzolt téglalap, melynek minden fala zárt. Ezen szobába zárt 2 dimenzióban élő ember vajon mekkora meglepetéssel fogadná, ha mi a papírra, a téglalapon belülre rajzolnánk egy asztalt. Mi egyszerűen átnyúlunk a 2 dimenziós fal felett, mert mi a harmadik dimenzióban is tudunk mozogni, de az ott élő 2 dimenziós ember azt tapasztalja mindebből, hogy a fal nem nyílt meg sehol, mégis a semmiből ott termett egy asztal. Képzeljük el ugyanezt a mi esetünkben. Egy zárt szobában vagyunk és ott terem egy asztal a szoba közepén, anélkül, hogy bárki bejött volna az ajtón, vagy akárhol. Bizony elég meglepő, de a negyedik dimenzióban mozogva épp így kerülhetnénk váratlan helyekre. Egyesek szerint a negyedik dimenzió létezése igenis valóság, melyre bizonyítékul szolgálnak a gömbvillámok, amik a negyedik dimenzió betüremkedései a mi dimenziónkba.
Az időt egy dimenziósnak ismerjük, melynek ráadásul iránya is van, így a térnél is nehezebb elképzelni több dimenziósnak, pedig az időutazáshoz szükségünk lesz rá. Ösztönösen megpróbálja az emberi agy a több dimenziós időt a tér több dimenziójához hasonlítani, ez azonban nem biztos, hogy helyes. Jó megközelítés lehet az, melyet a következő példával könnyebben meg lehet érteni: Képzeljünk el egy olyan ikerpárt, akiknek személyes időszerkezetük teljesen megegyezik, vagyis ugyanolyan korúak, mikor óvodába járnak, mikor elvégzik az iskolákat, mikor megkapják a diplomájukat, mikor összeházasodnak és épp ugyanannyi idősek mikor megszületik az első gyermekük, valamint ugyanannyi naposak, mikor meghalnak. Legyen ez a két testvér István és Béla. Az a furcsaság van kettejük kapcsolatában, hogy István úgy látja, hogy Bélával minden dupla olyan gyorsan történik. Ő még csak óvodás, mikor Béla iskolába jár, ő épphogy megkapja a diplomáját, de Bélának már gyerekei vannak és mire ő megházasodik, Béla jobb létre szenderült. Mintha Bélának fele annyi ideje lett volna élni, de István látta, hogy Bélával nemcsak gyorsabban történtek az események, hanem valóban gyorsabban is öregedett. Ez azonban nem elég: Béla mindezt pont fordítva látja. Úgy látja, hogy ő jár még épp iskolába, mikor István már a diplomáját veheti át, ő épp, hogy megházasodik, de István körül már az unokái futkosnak és míg ő csak az élete felén jár, ikertestvére már halott. Mindez úgy lehetséges, hogy a két ikertestvér különböző idődimenzióban él.
Mindkét testvér úgy látja, mintha a testvére csinálna mindent sokkal gyorsabban. Olyan, mintha egy mezőn két egymástól távol álló juhász nézne egymásra és mindkettő azt mondhatná a másikról, hogy milyen kicsi. Mindkettejüknek igaza van, hiszen a saját szemszögéből kicsinek látszik a másik, holott a valóságban aligha van köztük lényeges különbség. Ezen ikertestvéres példához készítettem egy ábrát, mely jól szemlélteti, hogy hogyan kell elképzelni a kétdimenziós időt, melyen ebben az esetben csak két külön idősíkot ábrázoltam, de végtelen lehetséges. Minél nagyobb az általuk bezárt szög, annál nagyobb az eltérés mértéke.

A képen látható mindkét testvér szemszögéből a másik eltérése, melynek mértéke épp akkora, hogy egymást dupla sebességgel lássák öregedni. A baloldali esetben például Béla C éves korában úgy látja, hogy István már B éves, ahol B=2C. Ugyanakkor István B éves korában Bélát A évesnek látja, ahol A=2B.
Az idő ilyen dimenzionálásával viszonylag egyszerűen lehetséges az időutazás: pusztán dimenziót kell váltani. A bal oldali szemszög szerint Béla úgy tud visszautazni a múltba, hogy A (legyen ez 32) éves korában indul István dimenziójába. Ekkor Bélának úgy tűnik, hogy István 2A (64) éves. Mikor odaér, akkor azonban nem a 64 éves Istvánnal találkozik, hanem a B (16) évessel. Ennek az az oka, hogy Istvánhoz a 32 éves Béla csak 16 éves korában érkezhet meg, hiszen István szemszögéből Béla öregszik dupla olyan gyorsan. Ugyanez történik, mikor Béla visszatér a saját dimenziójába: Csak akkor hagyhatta ott a 16 éves Istvánt, mikor Béla saját idődimenziójában 8 év telt el születése óta. Vagyis Béla visszajut a saját dimenziójába, indulásához képest 24 évvel korábbra (ekkor volt ő eredetileg 8 éves). Béla így az A-B-C utat teszi meg, ha a bal oldali ábrát tekintjük.
Persze ha végtelen idősík létezik, akkor tetszőleges lehet az időutazás távolsága, pusztán az idősíkok által bezárt szöget kell variálni.
Most már úgy is vehetjük, hogy megtaláltuk a múltba való időutazás egy lehetséges változatát, paradoxonok viszont továbbra is fennállnak. Azok kizárásához még tovább kell lépnünk a kétdimenziós idő szemléletünkről és a lehetséges időtopológiákkal kell foglalkoznunk. Mielőtt azonban ebbe belebonyolódnánk, tisztázzuk, hogy milyen problémák merülnek fel pontosan a múltba történő utazáskor. Először is tisztázni kell, hogy közvetlen kapcsolat nem lehet a külön idődimenziók között. Tehát a példában szereplő ikertestvérek nem léphetnének kapcsolatba egymással, csak időutazás révén. Elég arra gondolnunk, hogy ha a 32 éves Béla akar kérdezni valamit a 64 éves Istvántól, akkor a kérdést a 16 éves István kapja meg és válasza a 8 éves Bélához jut el. Itt pedig eljutunk a fő problémához, az ok okozati kapcsolat felborulásához. Vagyis Béla előbb kap választ, minthogy feltenné a kérdést: előbb következik be az okozat, mint az ok. A kétdimenziós idő feltétele tehát a visszafelé ható okság, legalábbis ha teljesen szabad időutazási lehetőségeket akarunk.
A filozófusok, amikor az időutazás és így a múltba történő utazás kapcsán felmerülő ellentmondásokról vitatkoztak, egy fontos megállapításra jutottak, mellyel kizárhatóvá tették a paradoxonok bekövetkeztét. Ez pedig az, hogyha az időt még nem is sikerült megismernünk teljesen és az többdimenziós, lehetővé téve az időutazást, akkor sem szeghetjük meg a világunk alapvető szabályait: nem tehetünk olyat, ami nem logikus (persze ezen lehetne vitatkozni, hogy az időutazás logikus-e, de több idődimenzió esetén igen). A térre egyszerű megérteni, hogy mi nem logikus: nem állhatok saját magam jobb oldalán, vagy nem lehetek saját magam szülője sem. Ha az időre is elfogadjuk ezeket a szabályokat, akkor nem következik be semmilyen ellentmondás. A nagypapa paradoxon esetén így ha visszautazik emberünk a múltba, hogy végezzen saját nagyapjával, akkor megpróbálhatja ugyan, de sikerülni semmiképpen sem fog neki (és másnak sem, egészen addig, amíg meg nem fogan hősünk szülője, aki majdan életet fog adni neki). Ezt azért köthetjük ki, mert eme tett legalább annyira nem felelne meg a logikának, mint a tér esetén említett példák.
A magyarázat elfogadhatónak tűnik, azt azonban észre kell vegyük, hogy ezzel jelentősen korlátozzuk a lehetőségeket. Ismét csak filozófiai kérdés, hogy ha vissza is tudunk utazni az időben, akkor ott mit tehetünk így? Ha ugyanis megpróbálunk csak szemlélőként ott járkálni, akkor is tudtunkon kívül befolyásolhatnánk dolgokat, amik eredetileg nem is történtek meg, vagyis szabályunk szerint nem változtathatjuk azt meg. Kérdés tehát, hogy mi számít változtatásnak. Például visszautazva a középkori Itáliába, miközben csodáljuk az ottani építészetet, az utcán meglát minket egy neves festő, aki aztán hazatérve emlékezetből megfesti a portrénkat. Vita tárgya máig is, hogy ebben az esetben a festmény valóban létezett valaha, csak mondjuk egy tűz miatt elpusztult és semmilyen feljegyzés nem maradt a létezéséről, vagy ezzel a tettel megváltoztatnánk a jövőt. Az idővel foglalkozó filozófusok egy része például úgy tartja, hogy a múlt nem is létezik, csak az emlékek által alkotott világ.
Ha a létezését nem is tagadjuk, de ezen elméletnek fontos része lehet az, hogy ha a múltban olyan tetteket hajtunk végre, amiknek következményeiről nem is tudunk, akkor semmi akadálya, hogy megtegyük. Ez alatt azt értem, hogy például nyilván nem lehetne visszautazni a második világháború kitörése elé néhány nappal, hogy megöljük Hitlert, mert ezzel jelentős változás történne a történelemben. Azt, viszont, hogy visszautazunk a dinoszauruszok korába, már nehezebb kizárni. Elképzelhető ugyanis, hogy a jövőben megalkotja az emberiség az időgépet, melynek segítségével elkezdenek visszautazni a dinoszauruszok közé nézelődni, azok viszont felfalják az összes látogatót. Ezzel az állatok jóllaknak, de igazán nem változtat semmit a helyzeten az emberek látogatása, mert kipusztul az összes őshüllő, így jelenlegi világunkban semmit sem befolyásol az eset.
Vannak azonban, akik tiltakoznak az ilyesfajta engedmények ellen is és azt állítják, hogy ha a világban a legapróbb változás is történik, akkor már ha kicsit is, és látszólag lényegtelen mértékben is, de megváltoztatjuk az események eredeti alakulását. Képzeljük el, hogy visszautazunk az időben és semmi mást nem teszünk, mint egy helyben állunk néhány másodpercig, majd távozunk is. Amíg ott álltunk, letapostuk a lábunk alatt lévő füvet, melyet eredetileg senki sem taposott le, tehát változást indukáltunk a világban. Ez a nézet tehát teljesen kizárja az időutazás lehetőségét. Fogadjuk el azonban akármelyik lehetőséget - vannak engedmények, vagy nincsenek -, a teljesen szabad időutazáshoz nem elegendő a kétdimenziós idő, hiszen túl sok logikailag lehetetlen dologgal kerülünk szembe. Így jutunk el a három dimenziós időhöz.
Az idő topológiáiról
Ehhez meg kell ismerkednünk az idő topológiájával. Tisztázzuk először, hogy mi az a "topológia" (aki tanult diszkrét matematikát, attól elnézést kérek a múlt felhánytorgatása miatt). A definícióját inkább mellőzöm, mert annak megértése is igen sok matematikai fogalom ismeretét feltételezi. Egyszerűbb megérteni egy példán keresztül. A topológia egy olyan geometriai tulajdonság, ami az összes közül a legabsztraktabb, így a legnehezebb elképzelni. Amikor valaminek a topológiáját vizsgáljuk, akkor eltekintünk minden metrikus, vagyis mérhető tulajdonságától. Nem számít az alakja, a mérete az adott testnek. Gumigeometriának is hívják, ennek oka pedig egy gyakran felhozott példa. Képzeljünk el egy befőttes gumit, melyet különböző méretű üvegre húzhatunk, a guminak változni fog a mérete, de a topológiája változatlan marad. Az alakhoz sem köthetjük, hiszen ha a gumit egy szögletes tejes dobozra húzunk, akkor annak veszi fel az alakját, de a topologikus tulajdonsága ekkor sem változik. Ha azonban elszakad a befőttes gumi, akkor megváltozik a topológiája is. Ha a topologikus tulajdonsága szerint vizsgáljuk, akkor semmi különbség sincs egy gumicsirke és egy traktor között. Ezen elvont szemléletre lesz éppen szükségünk az idő vizsgálatakor, hiszen el kell tekinteni minden térhez köthető tulajdonságtól.
Az idő lehetséges topológiáit egy viszonylag egyszerű topologikus ábrázolási móddal szemléltetünk, mégpedig a gráfokkal. A gráfok pontokból állnak, melyeket vonalakkal köthetünk össze, ezen vonalakat nevezzük éleknek. Az éleket úgy adhatjuk meg, hogy mely két pontot köti össze. Létezik irányított és irányítatlan él, melyet nyíllal jelölünk. Az élek alakja lényegtelen. A modern kozmogónia elég sok különböző idő topológiával foglalkozik, de nekünk elegendő lesz a következő hárommal foglalkozni, ezeket láthatjátok a következő ábrán.

Balról jobbra haladva a következő elnevezéseket használjuk: nyíl, karika és fa topológia. Az élek hossza lényegtelen, legfeljebb az áttekinthetőséget segíti. Mint említettem az élek alakja is jelentéktelen, tehát a nyílnak nem kell, hogy egyenes legyen, a karikának nem kell, hogy szabályos kör legyen. A fának különleges tulajdonságai vannak. Éleit választhattam volna irányítottaknak is, jelölésben ekkor a nyilak mindig felfele mutattak volna, de hogy miért is irányítatlanok, azt majd később megtudjátok. Fontos, hogy a fát jelen esetben lentről felfele kell vizsgálnunk (igazából a gyökértől a levelek felé kell nézni). A fa gyökere nem lehet szerteágazó, tehát egy pontból ered, az elágazások végein elhelyezkedő pontokat pedig leveleknek nevezzük (ahonnan nincs további elágazás).
Megszereztük a szükséges elméleti hátteret, hogy végre elkezdhessünk az idő topológiájáról beszélni. A nyíl topológia az, ami a jelenleg elfogadott idő szemléletet tükrözi. Vagyis teljesen lineárisan haladunk előre az időben. Két elméletet különböztethetünk meg itt is: a statikus és a dinamikus időszemléletet. Az ábra segítségével jól érthető a kettő közötti különbség, ugyanis a statikus időszemlélet szerint, ahogy haladunk előre az időben, úgy haladunk a nyíl egy részén a vége felé. Tehát e szerint véges az idő: volt kezdete és a nyíl végét elérve meg fog szűnni. A dinamikus időszemlélet szerint folyamatosan a nyíl végén haladunk és ahogy telnek a percek, úgy hosszabbodik ez a képzeletbeli nyíl (ebben az esetben nem lehetséges a jövőbe való utazás).
A karika topológián, mint látszik a nyíl körkörösen mutat, tehát az idő szüntelenül ismétli önmagát. Ezen elméletet látszik igazolni a folyton táguló világegyetem, melyben egyesek szerint egy pont után bekövetkezik újra egy ősrobbanás és minden kezdődik elölről. Az időutazás problémája itt leegyszerűsödik (persze a paradoxonok okozta problémák maradnak): képzeljük csak el, hogy Budapestről Bécsbe nem csak nyugatra indulva juthatunk el, hanem keletre is, csak sokkal hosszabb utat kell megtennünk. Tehát a karika idő topológia esetében, ha képesek vagyunk utazni a jövőbe, akkor elég sokat utazva a múltba jutunk. Ez az eredmény viszont problémát is jelent, mert megszűnik a jövő és múlt közti különbség. Elég arra gondolni, hogyha a jövőről beszélünk, akkor az egyben a múltunk is, ugyanakkor a múltunk a jövőnk.
Másik nagy probléma a karika topológiával, hogy nem egyértelmű az idő iránya. Az ábrán ugyan bejelöltem egy irányt, de az akár fordított is lehetne. Meghatározni nehéz az idő irányát, ebben az esetben lehetetlen, legfeljebb kiköthetjük, hogy legyen óramutató járásával egyező, vagy ellentétes. Azért állítom, hogy lehetetlen ebben az esetben meghatározni az idő irányát, mert létezik erre egy általánosan elfogadott elv. Ez pedig a már egyszer említett ok-okozati rendszer. Elengedhetetlen, hogy valaminek az oka előbb történjék időben, mint az okozata. Az pedig kizárt, hogy két partikuláris esemény oka legyen egymásnak (a kauzális reláció aszimmetrikus). A karika topológia esélyei ezzel jelentősen lecsökkentek, hiszen nem határozható meg egyértelműen az ok-okozati rendszer.
Maradt még a fa topológia, melynél a nyílhoz hasonlóan nemhogy nem gond az idő irányának meghatározása, hanem egyedülállóan, jelölés nélkül is nagyon jól látszik (ezért nem szokás az éleket irányítottnak venni). Arra, hogy hol következik be elágazás, leginkább kétféle magyarázat van. Az egyik szerint a természet törvényei határozzák meg az elágazásokat. Ez végtelen sok elágazást tesz lehetővé, hisz akár ha egy atomot tekintünk egy időpillanatban, akkor az vagy osztódik, vagy nem. Rögtön egy elágazást találtunk.
A másik elmélet szerint pont fordítva van: az elágazások írják le a természet törvényeit. Ez rengeteg lehetőséget vet fel, többek között a bennünket érdeklő időutazást is. Mindez azonban csak akkor lehetséges, ha a dinamikus időszemléletet fogadjuk el. Képzeljük csak el, hogy a történelmünk sokáig egy vonalon halad. Aztán mikor megalkot az emberiség egy időgépet, akkor visszautaznak vele a múltba. Ott nyilván változást indukálnak ezzel, így egy külön ágat hoznak létre. A megváltoztatott történelem azon az ágon halad tovább, amiből elindultak, az pedig marad változatlan. Így már semmilyen paradoxon, vagy ellentmondás nem állja utunkat. Egyedüli gond, hogy mint említettem a dinamikus időfelfogás szerint folyamatosan alakítjuk a jövőt, így nem lehetséges a jövőbe történő időutazás. Statikus időfelfogásnál megengedett a jövőbe való utazás, de az idő nem lehet fa topológiájú.
Ha elegyítjük a kétdimenziós és a fa topológiájú idő elméletét, akkor juthatunk a három dimenziós időhöz. Képzeljük el, hogy István és Béla idősíkjai ugyanúgy helyezkednek el, csak éppen az egésznek van mélységi kiterjedése is, ahol a fa ágai terebélyesednek. Ezzel a szemlélettel már kedvünk szerint utazhatunk vissza a múltba, az általunk indukált változások hatására újabb, alternatív dimenziókat hozunk létre. Azzal viszont számolni kell, hogy a jövőbe nem tudunk visszautazni (hacsak nem hibernálással, vagy idődilatációval lepörgetjük a szükséges időt).
Epilógus
Összegezve az egész gondolatmenetet, valószínűleg kétféle szerkezete és felépítése lehet az időnek. Egyik felfogás szerint a ma is ismert tulajdonságai (statikus/dinamikus és nyíl topológiájú) már a valóságot mutatják és megváltoztathatatlanok. Másik felfogás szerint dinamikus és fa topológiájú, lehetővé téve a múltba való időutazást. Igazából egyikre sincs bizonyítékunk. Nyilván minden jel az első elmélet helyességét látszik igazolni, de amíg nincs bizonyíték a második ellen, addig nem vethetjük el azt sem. Márpedig bizonyíték nincs, mert a korábban említett "miért nem jöttek már vissza az időben, hogy elmondják az időgép titkát" kérdésekre egyszerű a válasz. Visszajöttek és az idő egy másik ágán már 2006-ban is használják az időgépet. Azt, hogy valójában melyik szemlélet a helyes, tudniillik létezik időutazás, vagy sem, a fizika és a tudomány fejlődése idővel nyilván eldönti. Addig viszont úgy gondolom, hogy elég nagy a világunk ahhoz, hogy találjon mindenki magának ismeretlent. Miért akarnánk addig más időbe utazni, amíg a sajátunk is elég rejtéllyel szolgál?
Felhasznált irodalom:
Lewis - The Paradoxes of Time Travel
Judith Jarvis Thomson - A kétdimenziós idő példája
Newton-Smith, Chin-Steenrod, McCall, Von Wright, Reichenbach, H. Mellor elméletei
Csaba György Gábor - Kalandozás az égbolton
Lenin összes művei
Űrhajózási Lexikon
Felix R. Paturi - A technika krónikája
A világ körülöttünk - Beszélgetések a világról és törvényeiről
Kulin György - Mit mondanak a csillagok
Egely György - A titokzatos gömbvillám
Albert Einstein - On the electrodynamics of moving bodies
Max von Laue - Das relativitätsprinzip
Peter Pesic - Einstein and the twin paradox
Kempelen Farkas Digitális Tankönyvtár
Ambrus Attila József - Itt és most (értekezés a térről és időről)
Kapcsolódó cikkek




Reszletek a fohadiszallason, itt.
http://prohardver.hu/tema/vilagegyetem_osrobbanas_ter-ido_akit_erdekel_ide/friss.html
Ha nem vagy még tag, regisztrálj! 2 perc az egész.